通过 RLT 建立紧凑的 MIP 模型

混合整数规划（MIP）的一类基本解法是通过解它的线性松弛问题，进而逼近可行的整数最优解。令 F 为一个混合整数规划问题 MIP 的模型，LP(F) 为 F 的线性松弛后的可行域，conv(MIP)为 MIP 可行域的凸核（convex hull）。评价这个模型好不好通常需要看两点：LP(F) 有多接近 conv(MIP); LP(F) 的 size 是否足够小。

当然如果可以找到一个 F 使得 LP(F)=conv(MIP)，而且 F 的 size 是多项式级，那也太特么不可能发生在 NP-hard 问题上了。因为如果满足以上两点，解 F 只需要多项式时间，也就意味着宇宙级问题 P = NP 得到证实，人类马上就要崩坏了。（假如 P=NP，世界将会怎样？）

可以把凸核想象成 MIP 问题最最核心的可行域，假如达到了凸核，我们就可以很容易的求解问题。而 F 的线性松弛 LP(F) 一般是大过凸核的，那么一个思路就是如何一步一步的缩小（或者说紧化） LP(F)，直到 LP(F) = conv(MIP)。

RLT (Reformulation-Linearization Technique)算是一类缩小 LP(F) 的技术，而且已被证明应用 RLT 最终的结果正是 conv(MIP)。这类技术以前从未听说过，出于好奇，拿了个很简单的 MIP 问题做实验，结果还是很好的。后面会举个简单实例。RLT 的技术细节请参考以下书籍和论文：

Sherali, H. D., & Adams, W. P. (2013). A reformulation-linearization technique for solving discrete and continuous nonconvex problems (Vol. 31). Springer Science & Business Media.
Sherali, H. D., & Tuncbilek, C. H. (1992). A global optimization algorithm for polynomial programming problems using a reformulation-linearization technique. Journal of Global Optimization, 2(1), 101-112.
Sherali, H. D., & Alameddine, A. (1992). A new reformulation-linearization technique for bilinear programming problems. Journal of Global Optimization, 2(4), 379-410.

作者是我系教授 Dr. Sherali，貌似是我来的那年退休的。RLT 引起我的注意也是因为之前 Sherali 和老板写了几篇非对称旅行商问题 (ATSP) 的多项式模型的文章，他们用 RLT 紧化原始模型，效果挺好，感觉像魔法一样，特别犯规。

下面边举例边说明 RLT 的用法。因为 RLT 只涉及模型的 LP(F)的紧化，以下并不涉及目标函数。令

X=\{(x,y): x+y \leq 2 , -x+y \leq 1, 2x-2y\leq 1, x \mathrm{\ binary}, y\geq 0 \}.

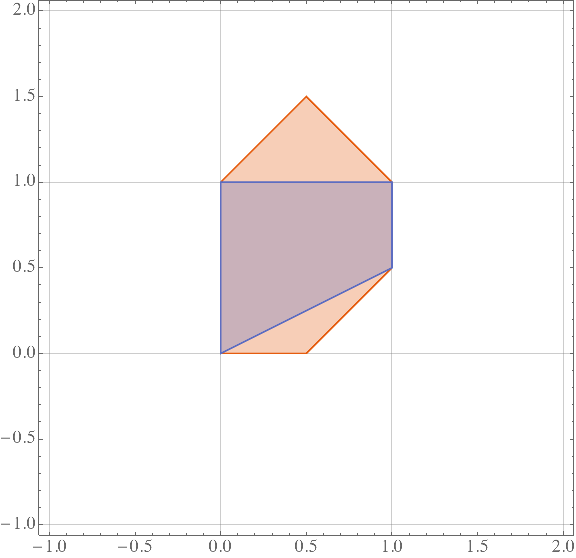
令 $X$ 对应的线性松弛可行域为 LP( $X$ )，它可以用下图表示。

image

横坐标是 $x$ ，纵坐标是 $y$ 。其中，中间深色区域为 $X$ 的凸核 conv( $X$ )，包裹凸核的橘色区域则是 LP( $X$ )。可以看到凸核 conv( $X$ )是一个梯形，梯形左右两个平行的底边则是真正的 $X$ 。

RLT 分为两步，reformulation 和 linearization。

第一步,reformulation

注意到因为 $x$ 是 binary，那么有以下三个式子成立

$x\\geq 0,$
$1-x \\geq 0,$
$x(1-x)=0 \\mathrm{\\ or \\} x^2=x.$

可行域 $X$ 除了 $x$ binary 以外的约束有四个，即 $x+y \\leq 2$ , $-x+y \\leq 1$ , $2x-2y\leq 1$ , 和 $y\\geq 0.$ 用 $x$ 和 $1-x$ 分别去乘以这四个不等式，并令 $v=xy$ (其实这个替换已经是 linearization 的一部分了)，我们可以得到以下八个不等式：

$ v \leq 2 x - x^2, v \leq x^2 + x, v \leq x^2 - 1.5 x + y + 0.5, v \leq y,$

$ v \geq -x^2 + 3 x + y - 2, v \geq x^2 + y - 1, v \geq x^2 - 0.5 x, v \geq 0.$

因为这八个不等式围起来的新的可行域多了 $v$ 这一维，所以我们用 Fourier-Motzkin elimination 把它投影到原来的 $(x,y)$ 空间。注意到上面的八个不等式分为了 $v\\leq$ 组和 $v\\geq$ 组，为了投影回原空间，需要使得每个 $v\\leq$ 组的不等式右手边大于等于每个 $v\\geq$ 组的右手边。如此，形成了 $4\times 4=16$ 个只包含 $x,y$ 的不等式，尽管有些不等式是冗余的。因为这 16 个不等式是从原先不等式推导得来的，所以新不等式围出的可行域（命名为 $X\_{P1}$ ）并不会比 LP(X) 更小。下图表示了这 16 个不等式以 4 个一分组所围成的区域，4 个区域的重合即为 $X\_{P1}$ ，恰巧等于 LP( $X$ ).

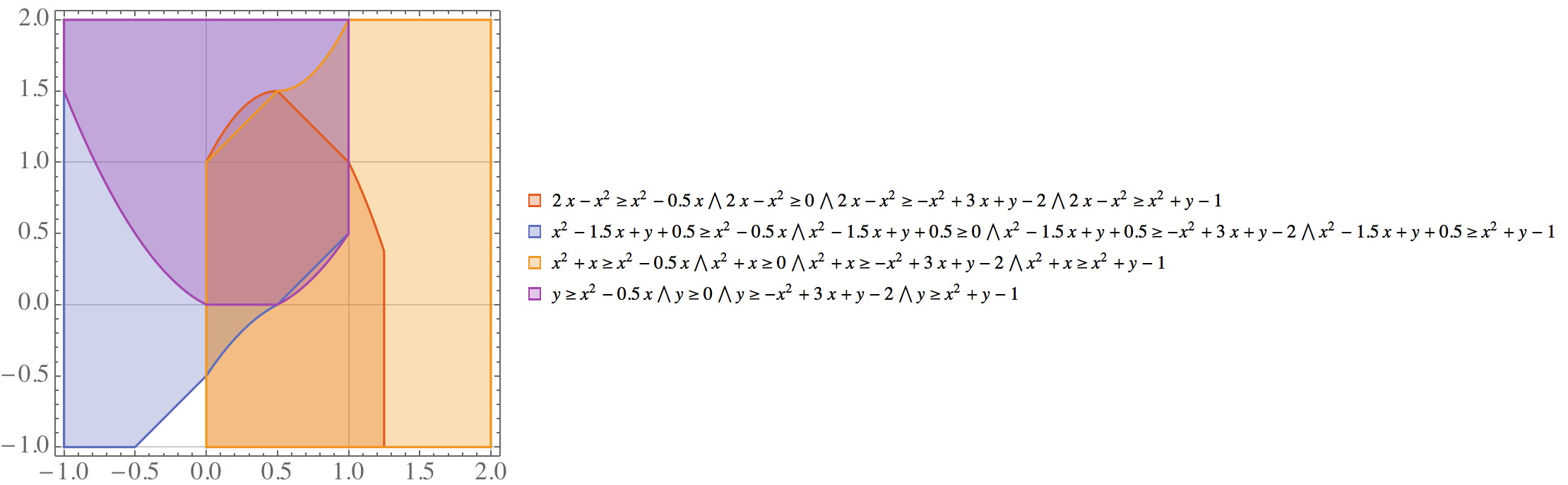image

注意到这些区域的边界并非纯直线，是因为二次项 $x^2$ 导致的。

第二步, linearization

这一步才是紧化可行域的关键。我们利用 $x^2=x$ ，把所有的二次项 $x^2$ 替换成 $x$ 。原先 16 个不等式围成的区域就变成了如下图所示：

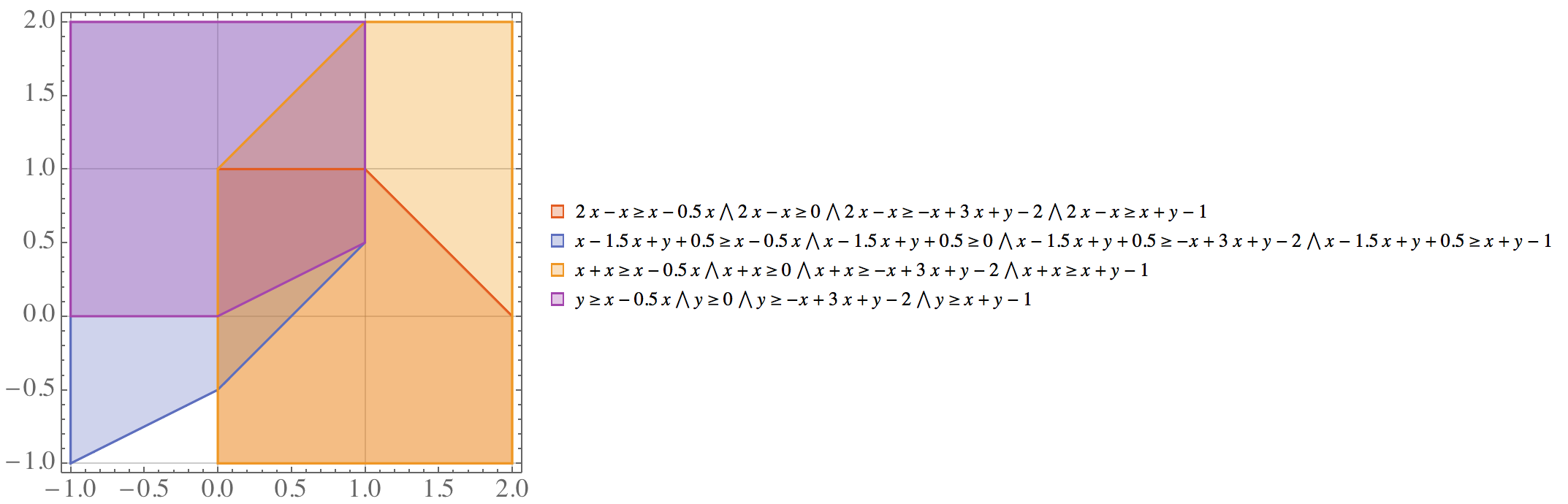image

4 个区域的重合是凸核 conv( $X$ )。去除冗余不等式，新的

X_{P1}=\{(x,y): x\leq 2y, 0\leq x\leq 1, y\leq 1\}

等于 conv( $X$ )。

本例运用的是一阶 RLT，所生成的模型一般命名成 RLT1。可以证明，如果 binary 变量只有一个（如本例），那么 LP(RLT1) 一定可以生成凸核。一般的情况是，如果有 $n$ 个 binary 变量，则有

\mathrm{LP(X)} \supseteq \mathrm{LP(RLT1)}\supseteq \mathrm{LP(RLT2)}\supseteq \dots \supseteq \mathrm{LP(RLTn)} = \mathrm{conv(}X\mathrm{)}.

RLT 最终可以生成凸核这个特点还是挺好的。它的缺点应该也可以看出来，就是生成的不等式的量会以指数级增长。有得有失，它在理论上的意义很重大，但是实际应用的时候还是需要一定的取舍，不可能全盘照搬。

文末附上作图用到的 Mathematica 的代码。