本文是自己学习凸优化的笔记和总结。挂在这里主要是方便自己查。当然，如果能帮到手滑点进来的人也是极好的。

本节关于凸函数和与之相关的一些性质。

下一集传送: 梯度下降法（无约束 + 光滑 + 凸函数）

Convex function

定义

ff is convex if

  1. dom ff is convex and
  2. (Jensen's inequality) αf(x)+βf(y)≥f(αx+βy)\alpha f(x) + \beta f(y) \geq f(\alpha x + \beta y) for all x,yx, y, for all α,β≥0\alpha, \beta \geq 0 s.t. α+β=1\alpha + \beta = 1.

一阶等价条件

For differentiable ff, ff is convex   ⟺  \iff

  1. dom ff is convex and
  2. f(y)≥f(x)+∇f(x)T(y−x)f(y) \geq f(x) + \nabla f(x)^T (y-x) for all x,yx, y.

一阶条件的几何意义是凸函数上任意点的切线都是凸函数的 under-estimator. 因为这个切线仿佛承接住了整个函数 ff， 所以又叫 supporting hyperplane.

二阶等价条件

For twice differentiable ff, ff is convex   ⟺  \iff

  1. dom ff is convex and
  2. ∇2f(x)⪰0\nabla^2 f(x) \succeq 0 for all xx.

二阶条件表明凸函数任意一点“曲度”都是凸的。也可以说梯度是单调的。

单调梯度等价条件

For differentiable ff, ff is convex   ⟺  \iff

  1. dom ff is convex and
  2. (∇f(x)−∇f(y))T(x−y)≥0\big (\nabla f(x) - \nabla f(y)\big )^T (x-y) \geq 0.

证明

  ⟹  \implies:
由一阶条件得

f(y)≥f(x)+∇f(x)T(y−x)f(y) \geq f(x) + \nabla f(x)^T (y-x)

f(x)≥f(y)+∇f(y)T(x−y)f(x) \geq f(y) + \nabla f(y)^T (x-y)

相加两式得证.
  ⟸  \impliedby:
定义 g(t)=f(x+t(y−x))g(t)=f(x+t(y-x)), 那么 g′(t)=∇f(x+t(y−x))T(y−x)g'(t)=\nabla f(x+t(y-x))^T (y-x).
那么对于 t≥0t \geq 0, 由于 (∇f(x)−∇f(y))T(x−y)≥0\big (\nabla f(x) - \nabla f(y)\big )^T (x-y) \geq 0 所以 g′(t)−g′(0)≥0g'(t)-g'(0)\geq 0.
那么 g(1)−g(0)=∫01g′(t)dt≥∫01g′(0)dt=g′(0)g(1)-g(0) = \int_0^1 g'(t) dt \geq \int_0^1 g'(0) dt = g'(0)
即 f(y)≥f(x)+∇f(x)T(y−x)f(y) \geq f(x) + \nabla f(x)^T (y-x) for all x,yx, y.

Lipschitz smooth

定义

ff is L-smooth if ∣∣∇f(x)−∇f(y)∣∣2≤L∣∣x−y∣∣2|| \nabla f(x) -\nabla f(y) || _2 \leq L || x-y || _2 for all x,yx, y.

L-smooth 表明一个函数的梯度的变化不会太突兀，或者说这个函数比较平滑。

等价条件

  1. ff is convex and L-smooth.
  2. (∇f(x)−∇f(y))T(x−y)≤L∣∣x−y∣∣22\big(\nabla f(x) -\nabla f(y)\big)^T(x-y) \leq L || x-y || _2^2 for all x,yx, y.
  3. g(x)=L2xTx−f(x)g(x)=\frac{L}{2} x^T x - f(x) is convex.
  4. (quadratic upper bound) 0≤f(y)−f(x)−∇f(x)T(y−x)≤L2∣∣x−y∣∣220 \leq f(y) - f(x) - \nabla f(x)^T (y-x) \leq \frac{L}{2} || x-y || _2^2
  5. f(y)≥f(x)+∇f(x)T(y−x)+12L∣∣∇f(x)−∇f(y)∣∣22f(y) \geq f(x) + \nabla f(x)^T (y-x) + \frac{1}{2L} || \nabla f(x) - \nabla f(y) || _2^2
  6. (co-coercivity) (∇f(x)−∇f(y))T(x−y)≥1L∣∣∇f(x)−∇f(y)∣∣22\big (\nabla f(x) - \nabla f(y)\big )^T (x-y) \geq \frac{1}{L} || \nabla f(x) - \nabla f(y) || _2^2.

证明

1  ⟹  21 \implies 2:

∣∣∇f(x)−∇f(y)∣∣2≤L∣∣x−y∣∣2∣∣∇f(x)−∇f(y)∣∣2⋅∣∣x−y∣∣2≤L∣∣x−y∣∣22(Cauchy-Schwartz)(∇f(x)−∇f(y))T(x−y)≤L∣∣x−y∣∣22\begin{aligned} || \nabla f(x) -\nabla f(y) || _2 &\leq L || x-y || _2\\ ||\nabla f(x) -\nabla f(y) || _2 \cdot || x-y || _2 &\leq L || x-y || _2^2 \\ \text{(Cauchy-Schwartz)} \quad \big(\nabla f(x) -\nabla f(y)\big)^T(x-y) &\leq L || x-y || _2^2 \end{aligned}

2  ⟺  32 \iff 3:

(∇f(x)−∇f(y))T(x−y)≤L∣∣x−y∣∣22=L(x−y)T(x−y)\big(\nabla f(x) -\nabla f(y)\big)^T(x-y) \leq L || x-y || _2^2 = L (x-y)^T (x-y)

(Lx−∇f(x)−Ly+∇f(y))T(x−y)≥0\big(Lx-\nabla f(x) - Ly+\nabla f(y) \big)^T(x-y) \geq 0

即 (∇g(x)−∇g(y))T(x−y)≥0\big (\nabla g(x) - \nabla g(y)\big )^T (x-y) \geq 0,
由单调梯度条件， gg 是 convex.

3  ⟺  43 \iff 4: 利用 gg 为 convex 的一阶条件。

4  ⟹  54 \implies 5:
令 z=y+1L(∇f(x)−∇f(y))z=y+\frac{1}{L}(\nabla f(x)-\nabla f(y)).

f(y)−f(x)=f(y)−f(z)+f(z)−f(x)(quadratic upper bound)≥−∇f(y)T(z−y)−L2∣∣y−z∣∣22+∇f(x)T(z−x)(substitute z)≥−1L∇f(y)T(∇f(x)−∇f(y))−12L∣∣∇f(x)−∇f(y)∣∣22+∇f(x)T(y−x)+1L∇f(x)T(∇f(x)−∇f(y))=∇f(x)T(y−x)+12L∣∣∇f(x)−∇f(y)∣∣22\begin{aligned} f(y)-f(x) &= f(y) - f(z) + f(z) - f(x) \\ \href{./# 等价条件}{\text{(quadratic upper bound)}} \quad &\geq -\nabla f(y)^T(z-y) - \frac{L}{2} ||y-z||_2^2 + \nabla f(x)^T (z-x) \\ \text{(substitute z)} \quad &\geq -\frac{1}{L}\nabla f(y)^T (\nabla f(x)-\nabla f(y)) \\ & \qquad - \frac{1}{2L} ||\nabla f(x)-\nabla f(y)||_2^2 + \nabla f(x)^T (y-x) \\ & \qquad + \frac{1}{L}\nabla f(x)^T (\nabla f(x)-\nabla f(y)) \\ &= \nabla f(x)^T (y-x) + \frac{1}{2L} ||\nabla f(x)-\nabla f(y)||_2^2 \end{aligned}

5  ⟹  65 \implies 6:
由 5，

f(y)≥f(x)+∇f(x)T(y−x)+12L∣∣∇f(x)−∇f(y)∣∣22f(y) \geq f(x) + \nabla f(x)^T (y-x) + \frac{1}{2L} || \nabla f(x) - \nabla f(y) || _2^2

f(x)≥f(y)+∇f(y)T(x−y)+12L∣∣∇f(x)−∇f(y)∣∣22f(x) \geq f(y) + \nabla f(y)^T (x-y) + \frac{1}{2L} || \nabla f(x) - \nabla f(y) || _2^2

两式相加得 6.

6  ⟹  16 \implies 1:
对 6 的左边使用 Cauchy-Schwartz 不等式可得 L-smooth.
6 的右边 ≥0\geq 0， 使用单调梯度可得 convex.

从几何上理解 L-smooth 函数，ff 的下界为超平面，上界为二次函数。如下图所示。

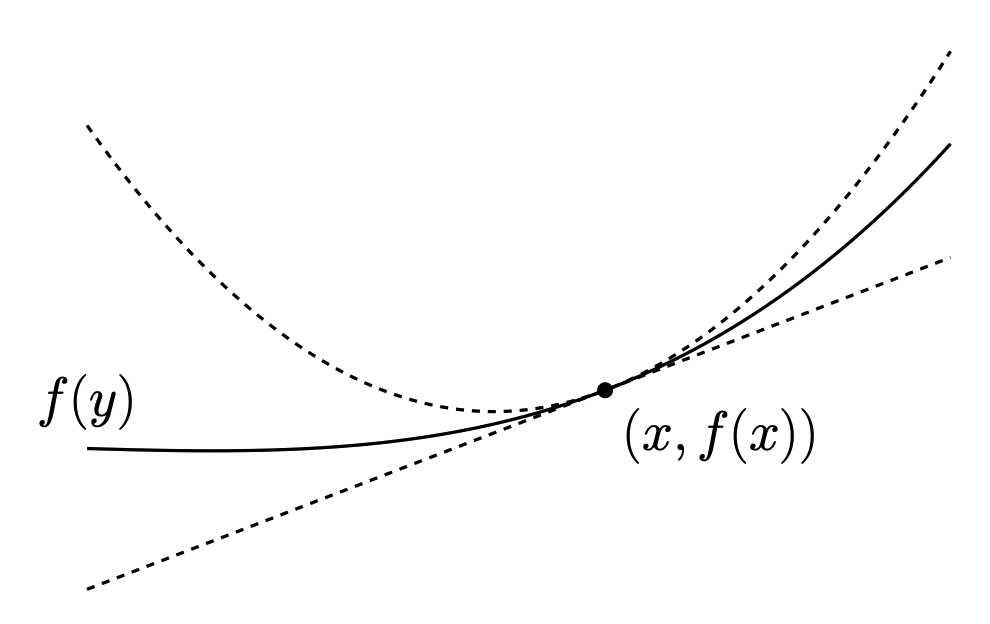L-smooth 函数L-smooth 函数

Strongly convex

定义

ff is μ\mu-strongly convex if f(x)−μ2xTxf(x)-\frac{\mu}{2}x^T x is convex.

一个函数减去二次函数仍然是 convex, 说明它至少有这个二次函数这么凸。或者说这个二次函数是它的一个下界。如下图所示。

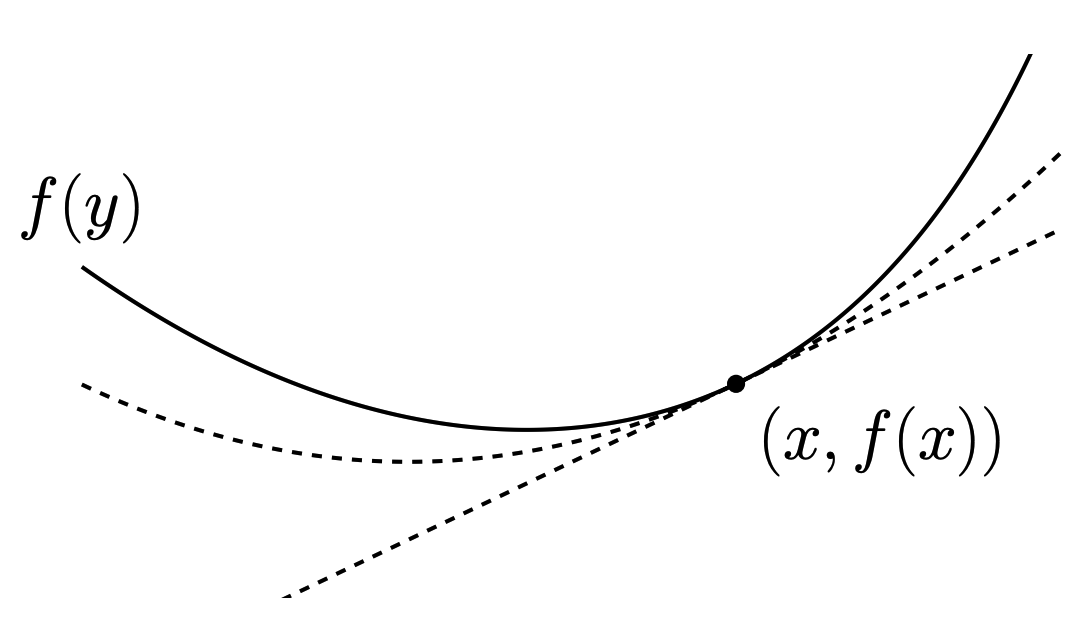Strong convex 函数Strong convex 函数

等价条件

  1. f​f​ is differentiable and μ​\mu​-strongly convex.
  2. ff is differentiable and f(αx+βy)≤αf(x)+βf(y)−μαβ2∣∣x−y∣∣22f(\alpha x +\beta y) \leq \alpha f(x) + \beta f(y) - \frac{\mu \alpha \beta}{2} ||x-y||_2^2 for all x,yx, y, for all α,β≥0\alpha, \beta \geq 0 s.t. α+β=1\alpha + \beta = 1.
  3. (quadratic lower bound) f(y)≥f(x)+∇f(x)T(y−x)+μ2∣∣y−x∣∣22f(y)\geq f(x) + \nabla f(x)^T (y-x) + \frac{\mu}{2} ||y-x||_2^2.
  4. (strong monotonicity or coercivity) (∇f(x)−∇f(y))T(x−y)≥μ∣∣x−y∣∣22\big (\nabla f(x) - \nabla f(y)\big )^T (x-y) \geq \mu|| x - y || _2^2.

证明

$1 \iff 2 $: 使用 convex 函数定义.
$1 \iff 3 $: 使用 convex 函数的一阶条件.
$1 \iff 4 $: 使用 convex 函数的单调梯度条件.

References

  1. Lecture notes: Gradient method. EE236C - Optimization Methods for Large-Scale Systems (Spring 2016). Vandenberghe, UCLA.

  2. Zhou, X. (2018). On the Fenchel Duality between Strong Convexity and Lipschitz Continuous Gradient. arXiv preprint arXiv:1803.06573.